Fast Fingerprint Identification for Large Databases
This Website contains complementary material to the paper:
D. Peralta, I. Triguero, R. Sanchez-Reillo, F. Herrera, and J.M. Benítez, Fast Fingerprint Identification for Large Databases.
Source code
The source code for the proposal described in this paper can be found at https://github.com/dperaltac/mpi-afis/.
Summary
Abstract
Fingerprint matching has emerged as an effective tool for human recognition due to the uniqueness, universality and invariability of fingerprints. Many different approaches have been proposed in the literature to determine faithfully if two fingerprint images belong to the same person. Among them, minutiae-based matchers highlight as the most relevant techniques because of their discriminative capabilities, providing precise results. However, performing a fingerprint identification over a large database can be an inefficient task due to the lack of scalability and high computing times of fingerprint matching algorithms.
In this paper, we propose a distributed framework for fingerprint matching to tackle large databases in a reasonable time. It provides a general scheme for any kind of matcher, so that its precision is preserved and its time of response can be reduced.
To test the proposed system, we conduct an extensive study that involves both synthetic and captured fingerprint databases, which have different characteristics, analyzing the performance of three well-known minutiae-based matchers within the designed framework. With the available hardware resources, our distributed model is able to address up to 400 000 fingerprints in approximately half a second.
Additional Background
Precision measures
Fingerprint recognition can be divided into two different problems: verification, which is a 1:1 comparison, and identification, which involves a search in a database and thus a 1:N comparison. This paper focuses on identification, which is the most complex of them.
The identification problem can be seen as a verification performed once per each fingerprint in the database. The main difference between these problems is therefore a matter of complexity order. The objective in a verification problem is to obtain a very precise result, reducing the error rate as much as possible. However, complex verification methods are not useful for identification because the overall response time would be excessive. Furthermore, an accurate identification is much more difficult to achieve because a single successful identification implies N correct verifications, and a single failure can mean a wrong identification.
The result of an identification request can be one of these four types.
- Positive (P): when the correct identity is found.
- False Positive (FP): when an incorrect identity is returned.
- Rejected (R): when the input fingerprint (called impostor) is not in the database , and the system returns a "not found" message.
- False rejected (FR): when the input fingerprint (called genuine) does exist in the database, but the system returns a "not found" message.
Thus, the total number of requests is the sum of these four response types as shown in the following equation:
$$N_T = N_P + N_{FP} + N_R + N_{FR}$$
The two main accuracy measures are the False Acceptance Rate (FAR) and the False Rejection Rate (FRR), which are respectively the proportion of FP and FR identifications over the set of NT requests.
Stopping criteria
Supposing a database with N template fingerprints, p slave processes and h threads per slave, each thread has to perform N/(ph) executions of the matching algorithm in order to identify an input fingerprint. The proposed distributed identification system includes several stopping criteria for the search:
- Maximum score: each slave process sends the best found score among the fingerprints in the database, and the master returns the fingerprint with the best score among all slaves. The penetration rate is always 100%.
- No stop: the slave processes send to the master all the fingerprints that have a matching score above a given threshold. Therefore, the number of fingerprints returned by a slave can be between 0 and N/p, and the penetration rate is always 100%. The master process returns to the user all the matchings it receives, i.e., all the fingerprints whose matching score with the input fingerprint is above the given threshold. A very promising environment for this configuration is the use of a very fast matching algorithm to extract a set of candidate template fingerprints that are similar to the input. Then, a very precise algorithm can be used for searching in this small set, with much less time restrictions than in the whole database.
- Stop: a slave process stops the search when any of its threads finds a template fingerprint with a matching score above a threshold. Then, the slave performs two actions:
- It sends the found match to the master process, which returns it immediately to the user.
- It sends a signal to all the other slaves, ordering them to stop the search because a match has already been found.
This configuration allows the reduction of the penetration rate. In an ideal situation, the identification of a genuine fingerprint would have a penetration rate of 50%, and an impostor fingerprint would require the exploration of the full database in order to ensure that no fingerprint matches with it. However, in practice this is impossible to achieve, and this kind of stop criteria is very prone to errors, as two similar fingerprints can be considered the same if their score is high enough without checking the rest of the database for fingerprints with an even higher score. Similarly, if the input fingerprint has significant differences with its template copy (translations, rotations, environment conditions as humidity, scars...) the search in the database can produce a "not found" results if the score is not high enough.
The use of thresholds in the identification requires a deep study of the fingerprint features and the matching algorithm behavior, as the identification systems are very sensitive to small variations of the threshold. The environment conditions (humidity, temperature, skin state...) modify the shape of the input fingerprint and thus have certain effects on the score when it is compared to other fingerprints. A single outlier (be it a low genuine score or a high impostor score) can cause the whole identification to be wrong, so this problem is not trivial.
Experimental framework
Fingerprint databases
A correct scalability study requires a very large database. However, there is no public captured fingerprint database big enough to cover this need, so we used SFinGe to generate a database with 400,000 synthetic fingerprints, using the parameters described in the following table to ensure the generation of realistic fingerprints:
Scanner parameters
- Acquisition area: 0.58" x 0.77" (14.6mm x 19.6mm).
- Resolution: 500 dpi.
- Image size: 288 x 384.
- Background type: Optical.
- Background noise: Default.
- Crop borders: 0 x 0.
Generation parameters
- Impression per finger: 25.
- Class distribution: Natural.
- Set all distributions as: "Varying quality and perturbations".
- Generate pores: enabled.
- Save ISO templates: enabled.
Output settings
- Output file type: WSQ.
Table 1. Parameter specification used with the SFinGe tool
SFinGe randomly generates the fingerprint minutiae and calculate a fingerprint image from them, following patterns so that the resulting synthetic fingerprints behave as natural captures. As SFinGe is able to provide the generated minutiae as an additional output, this paper has used both the returned ground-truth minutiae and the extracted minutiae (using mindtct), obtaining two databases with the same fingerprints but slightly different characteristics.
For each fingerprint 25 impressions have been generated. To perform a more realistic setup, we carry out an enrollment process, which consists of selecting a single template impression with a minimum of 40 minutiae for each fingerprint. When all 25 impressions of a fingerprint have less have less than 40 minutiae, the copy with the highest number of minutiae is taken as template. The remaining 24 copies are considered candidate input fingerprints. Then, several subsets of the whole template database (each of them of increasing sizes) have been selected, respecting the natural class distribution, in such a way that each database contains the immediately smaller one. Therefore, each database is contained in all the bigger ones. The size of all database subsets are presented in Tables 2 and 3, along with the minutiae statistics for both template and input fingerprints. As it can be seen, the number of average minutiae is higher for the extracted feature vectors due to the noise introduced by the image generation and the processing steps. This implies that mindtct extracts an average of 15 spurious minutiae per fingerprint.
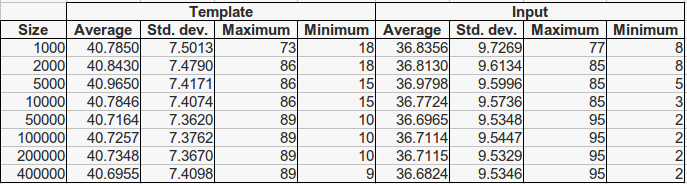
Table 2. Minutiae statistics for fingerprints in the SFinGe ground-truth database

Table 3. Minutiae statistics for fingerprints in the SFinGe extracted database
Finally, we have selected a subset of input fingerprints by choosing one random input impression of each fingerprint in the database of size 1,000, obtaining a single test set of 1,000 input fingerprints. As the 1,000 fingerprints database is included in all databases of bigger size, this test set can be used for all the generated databases, providing similar test conditions for all experiments.
Algorithms and parameters
Three different matching algorithms of the state-of-the-art literature have been used within the framework:
- Jiang is a classical hybrid matching algorithm. Each minutia is described with a feature vector that depends on its neighboring minutiae, and the feature vectors of both fingerprints are compared in pairs. The algorithm assumes that the most similar pair corresponds to the same minutia in both fingerprints and compares the rest of the fingerprint using relative coordinates and angles (avoiding the translation and rotation problems).
- Chen focuses on getting robustness despite of the fingerprint distortion. The algorithm is mostly local, as it calculates the local topology for each minutiae given a fixed radius. Then, it compares the local topologies of both fingerprints, and if they are similar enough, it repeats the comparison with a modified radius to avoid problems with the image distortion.
- Minutia-Cylinder-Code (MCC) uses both local and global information to perform the matching. For each minutia, a tridimensional cylinder is build and discretized in cells. Each cell is given a value that depends on its position and the relative position of neighboring minutiae. According to this number, the cell can be declared either valid or invalid, so that only cylinders with a minimum number of valid cells are taken into account for the matching process. This process compares the cylinders of both fingerprints cell by cell and merges the results (global matching) to get the score.
- This algorithm has a binary and a real version. In this paper, we focus on the latter, which is more precise and more suited for general purpose machines. In the paper we select 16 cells as the cylinder side size in order to get the most accurate configuration, which is also the most computationally complex. In this web site, we also show the results for the configuration with 8 cells, which is les complex and thus faster.
All four algorithms (Jiang, Chen, MCC8 and MCC16) have been developed by the authors of this paper, with the only help of the information shown at each of the referred papers. All the used methods parameters are common for all databases, and they were selected according to the recommendation of the corresponding authors:

Table 4. Parameters for the methods used in the experimentation.
Results obtained
Efficiency results
The four described algorithms have been executed over the respective subsets of three described databases. Each execution consisted in 1,000 identifications in a single database, and the presented times are the average of these 1,000 identifications. All presented speedups are measured in relation to the sequential identification time in the same database.
Efficiency results for all databases with Jiang, Chen, MCC8 and MCC16 ![]()
![]()
Precision results
This section contains the precision results obtained in the described executions. Thus, we present for each database the number of Positive and False Positive identifications, when the system uses the maximum score stopping criteria. Note that these results are independent from the number of nodes and threads because the system logic is the same in all cases, ensuring the same precision of the sequencial version.
Precision results for SFinGe ground-truth and some SFinGe extracted databases with Jiang, Chen, MCC8 and MCC16 ![]()
![]()
